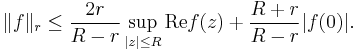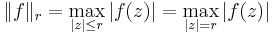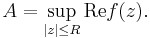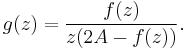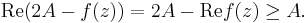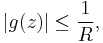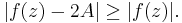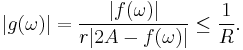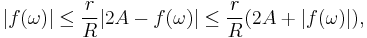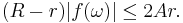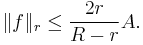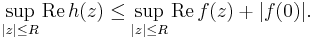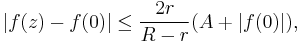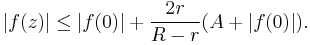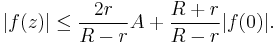Borel–Carathéodory theorem

In mathematics, the Borel–Carathéodory theorem in complex analysis shows that an analytic function may be bounded by its real part. It is an application of the maximum modulus principle. It is named for Émile Borel and Constantin Carathéodory.

Statement of the theorem

Let a function f be analytic on a closed disc of radius R centered at the origin. Suppose that r < R. Then, we have the following inequality:

\|f\|_r \le \frac{2r}{R-r} \sup_{|z| \le R} \operatorname{Re} f(z) %2B \frac{R%2Br}{R-r} |f(0)|.

Here, the norm on the left-hand side denotes the maximum value of f in the closed disc:

\|f\|_r = \max_{|z| \le r} |f(z)| = \max_{|z| = r} |f(z)|

(where the last equality is due to the maximum modulus principle).

Proof

Define A by

A = \sup_{|z| \le R} \operatorname{Re} f(z).

First, assume that 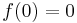f(0) = 0. If f is identically zero, then the theorem is trivially true. If f is not identically zero, then A > 0. Define the function g by

g(z) = \frac{f(z)}{z(2A-f(z))}.

The function g has a removable singularity at z = 0. Furthermore, the factor 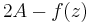2A - f(z) is nonzero when |z| ≤ R, because

\operatorname{Re}(2A-f(z)) = 2A - \operatorname{Re} f(z) \ge A.

Therefore, g is analytic in the disc { z ∈ C : |z| ≤ R }. If z is on the boundary of this disc, then

|g(z)| \le \frac{1}{R},

because

|f(z)-2A| \ge |f(z)|.

Since g is analytic, we can apply the maximum modulus principle to find that |g(z)| ≤ 1/R for all z with |z| ≤ R.

Now, suppose that ω is a complex number with 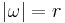|\omega| = r. Then

|g(\omega)| = \frac{|f(\omega)|}{r|2A-f(\omega)|} \le \frac{1}{R}.

So

|f(\omega)| \le \frac{r}{R} |2A-f(\omega)| \le \frac{r}{R} (2A%2B|f(\omega)|),

whence

(R-r) |f(\omega)| \le 2Ar.

Thus,

\|f\|_r \le \frac{2r}{R-r} A.

In the general case, where f(0) does not necessarily vanish, let 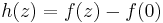h(z) = f(z) - f(0). Then, by the triangle inequality,

\sup_{|z| \le R} \operatorname{Re} \, h(z) \le \sup_{|z| \le R} \operatorname{Re} \, f(z) %2B |f(0)|.

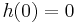Because h(0) = 0, we can say that

|f(z)-f(0)| \le \frac{2r}{R-r} (A%2B|f(0)|),

if |z| ≤ r. Furthermore,

|f(z)-f(0)| \ge |f(z)| - |f(0)|,

so

|f(z)| \le |f(0)| %2B \frac{2r}{R-r} (A%2B|f(0)|).

Therefore,

|f(z)| \le \frac{2r}{R-r} A %2B \frac{R%2Br}{R-r} |f(0)|.

This completes the proof.

References